forest

Last updated January 25, 2005

Background

A forest is a node-based (bidirectional) data structure for the representation of a heirarchy. The parent/child relationship between the nodes is maintained in the container class, so any regular type can be stored within without affecting it. It is equipped with a host of powerful iterators for varied methods of traversing the heirarchy, each of which is described below.

Usage

An Empty Forest

The best way to describe the forest class and its iterators is visually. Here is what a forest with no nodes added to it looks like (an "empty" forest):

The "forest" is simply the item you "hang on to" when you're creating forest nodes. Note that subtrees themselves, then, are not forests.

Forest Iteration

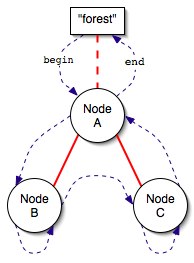
Here's a simple forest with some nodes added:

In this figure we have a forest with three nodes. The red lines are the tree structure of the forest- node A connects to both nodes B and C as children. The blue dashed lines are the possible "positions" the forest::iterator will be over this forest. The best way to think of the forest::iterators is not so much the node that they point to but rather the nodes they "sit" in between. For instance, forest::begin() "sits" in between the forest head and node A in the above example.

A Sample Iteration

To follow a forward fullorder iterator over the above example, we start between forest head and A. The iterator will then move onto node B, where something interesting happens. You'll see a "pivot" take place where the iterator doesn't actually move on from node B to C. Instead, it "changes edges", notably from the leading edge of node B to the trailing edge of B. The next step takes us to the leading edge of C, then another pivot to the trailing edge of C. The iterator will then move back up to A's trailing edge, then to the top, forest::end().

Visiting a node twice in every iteration of a forest is very useful in the case of serialization of the forest data, especially to XML-based formats. Upon leading-edge arrival to the node you output the opening (<>) tag and upon trailing-edge arrival you output the closing (</>) tag. Since the (sub)children are visited in between these two arrivals the output will be well-formed XML that perfectly describes the state and relationships of the forest nodes.

forest::iterator Types

There are several types of iterators available to adobe::forest. They are:

• forest::iterator: (also known as the fullorder iterator.) Visits the nodes by <parent><children><children><parent>. Each node in the forest is visted twice.
• forest::preorder_iterator: Visits the nodes by <parent><children>. Each node in the forest is visted once.
• forest::postorder_iterator: Visits the nodes by <children><parent>. Each node in the forest is visted once.
• forest::child_iterator: From any given node, child_iterator is a bidirectional iterator that walks a range of siblings (not the node's children) by "pivoting" on each node. There is a child_begin() and child_end() function to give you a range for the children of any node. Thus the child_iterator only applies to the first level of siblings, not to grandchildren or beyond.

There are also reverse_ versions of the fullorder and child iterators, and const_ versions of the fullorder and child iterators.

Note that only the fullorder iterator and child iterator are guaranteed constant time for increment and decrement. Pre- and post-order are amortorized constant time for a full traversal, but any single increment could take up to O(N) where N is the number of nodes in the forest.

Node Insertion

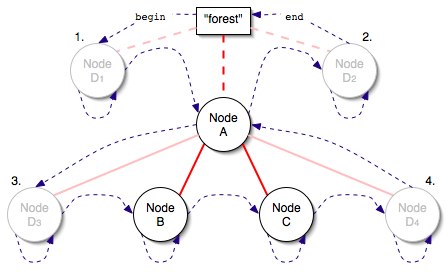
Consider the simple forest example above. Now let's say we wanted to insert a new node, D, somewhere around any given node in the tree (in this case we'll use node A). Given node A there are four distinct relationships D will have to A after insertion. The four possible relationships are:

1. As the previous sibling to A. Note the iterator is pointing to A.
2. As the next sibling to A. Note the iterator is pointing to forest::end().
3. As the first child of A, or the previous sibling of B. Note the iterator is pointing to B.
4. As the last child of A, or the next sibling of C. Note the iterator is pointing to A.

Observe that the last two relationships are similar to the first two. Consider this visual of the above situation:

Note that for each of the four possibilities, the new node will be inserted along one of the dashed lines leading into or out of A. Don't forget that the dashed lines represent the position of any given iterator at any given time in the forest. In the case of a leaf node, the leading out and trailing in lines (iterator positions) are the same line (the loop), so the principle still applies. Insertion of nodes will always take place on top of one of these dashed lines, and never anywhere else.

There is an insert which takes a [first, last) sequence, allowing you to insert more than one node essentially at the same location. Doing so makes the inserted sequence all "siblinging" on the same arc. It is the same as if you inserted each item, first to last - 1, at the same location. So let's say I have a fullorder iterator to the leading edge of node A and I want to add a vector of items as children of A. One can write:

// move my iterator to exit the leading edge
++iter;
 
// add all of the vector as children of A.
my_forest.insert(iter, my_vec.begin(), my_vec.end()); 

Observe that if you did not do the initial ++iter the vector's elements would be added before A, as siblings of A.

Node Deletion

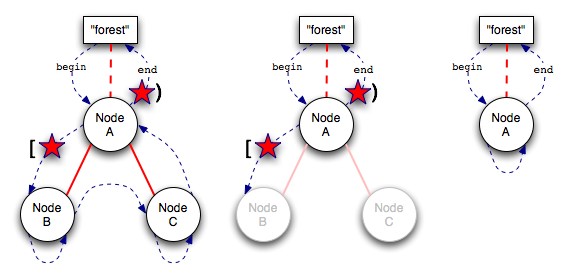
Deletion of nodes happens by the passing of two iterators. Nodes can only be deleted if they are leaf nodes. If the iterators encompass a range of nodes, the nodes will be deleted bottom-up, so they are always leaf nodes when they are deleted. The rule for the deletion of nodes is this: a node will be deleted if and only if the deletion iteration passes through the node twice. As an example consider the following diagrams:

In the first stage we have the iterators sitting between A and B and at forest::end(). The nodes B and C will be deleted because the iterator will go through both of those nodes twice while traversing from the start to the end of the deletion range. Note that even though the deletion iterator will pass through A it is not deleted because it only passes through once. Another way to think about it is if you were to "pinch" the forest with you fingers at the start and end of the range, and any node that isn't held back by the pinching at those two locations "drops" off the forest and is deleted. In the above case A would be dropped by one of the pinches but not the other, so it remains.

Examples

In the following sections, the code below is used for output:

template <typename R> // R is a depth adaptor range
void output(const R& f)
{
    typedef typename boost::range_iterator<R>::type iterator;
 
    for (iterator first(boost::begin(f)), last(boost::end(f)); first != last; ++first)
    {
        for (typename iterator::difference_type i(first.depth()); i != 0; --i)
        {
            std::cout << "\t";
        }
        if (first.edge() == adobe::forest_leading_edge)
        {
            std::cout << "<" << *first << ">" << std::endl;
        }
        else
        {
            std::cout << "</" << *first << ">" << std::endl;
        }
    }
}

Default Construction and Insert

typedef adobe::forest<std::string> forest;
typedef forest::iterator iterator;
 
forest f;
iterator i (f.begin());
i = adobe::trailing_of(f.insert(i, "grandmother"));
{
    iterator p (adobe::trailing_of(f.insert(i, "mother")));
    f.insert(p, "me");
    f.insert(p, "sister");
    f.insert(p, "brother");
}
{
    iterator p (adobe::trailing_of(f.insert(i, "aunt")));
    f.insert(p, "cousin");
}
f.insert(i, "uncle");
 
output(adobe::depth_range(f));

Results:

<grandmother>
    <mother>
        <me>
        </me>
        <sister>
        </sister>
        <brother>
        </brother>
    </mother>
    <aunt>
        <cousin>
        </cousin>
    </aunt>
    <uncle>
    </uncle>
</grandmother>

Copy Construction and Reverse

// This code picks up where the "Default Construction and Insert" example left off.
 
forest f2(f);
iterator f2_grandmother(adobe::find(adobe::preorder_range(f2), "grandmother").base());
f2.reverse(adobe::child_begin(f2_grandmother), adobe::child_end(f2_grandmother));
 
output(adobe::depth_range(f2));

Results:

<grandmother>
    <uncle>
    </uncle>
    <aunt>
        <cousin>
        </cousin>
    </aunt>
    <mother>
        <me>
        </me>
        <sister>
        </sister>
        <brother>
        </brother>
    </mother>
</grandmother>

Reverse Iterator

// This code picks up where the "Default Construction and Insert" example left off.
 
output(adobe::depth_range(adobe::reverse_fullorder_range(f)));

Results:

<grandmother>
    <uncle>
    </uncle>
    <aunt>
        <cousin>
        </cousin>
    </aunt>
    <mother>
        <brother>
        </brother>
        <sister>
        </sister>
        <me>
        </me>
    </mother>
</grandmother>

Node Deletion

// This code picks up where the "Default Construction and Insert" example left off.
 
forest f3(f);
iterator f3_aunt(adobe::find(adobe::preorder_range(f3), "aunt").base());
iterator f3_uncle(adobe::find(adobe::preorder_range(f3), "uncle").base());
f3.erase(adobe::leading_of(f3_aunt), ++(adobe::trailing_of(f3_uncle)));
 
output(adobe::depth_range(f3));

Results:

<grandmother>
    <mother>
        <me>
        </me>
        <sister>
        </sister>
        <brother>
        </brother>
    </mother>
</grandmother>

Splicing As Siblings to A Node

// This code picks up where the "Default Construction and Insert" example left off.
 
forest f4(f);
forest f5(f);
iterator f4_aunt(adobe::find(adobe::preorder_range(f4), "aunt").base());
 
std::cout << "Size of f4 pre-splice: " << f4.size() << std::endl;
std::cout << "Size of f5 pre-splice: " << f5.size() << std::endl;
 
// Note that because f4_aunt is on the leading edge, the spliced forest's
// top nodes will be siblings to f4_aunt.
 
f4.splice(f4_aunt, f5);    
 
output(adobe::depth_range(f4));
 
std::cout << "Size of f4 post-splice: " << f4.size() << std::endl;
std::cout << "Size of f5 post-splice: " << f5.size() << std::endl;

Results:

Size of f4 pre-splice: 8
Size of f5 pre-splice: 8
<grandmother>
    <mother>
        <me>
        </me>
        <sister>
        </sister>
        <brother>
        </brother>
    </mother>
    <grandmother>
        <mother>
            <me>
            </me>
            <sister>
            </sister>
            <brother>
            </brother>
        </mother>
        <aunt>
            <cousin>
            </cousin>
        </aunt>
        <uncle>
        </uncle>
    </grandmother>
    <aunt>
        <cousin>
        </cousin>
    </aunt>
    <uncle>
    </uncle>
</grandmother>
Size of f4 post-splice: 16
Size of f5 post-splice: 0

Splicing As Children to A Node

// This code picks up where the "Default Construction and Insert" example left off.
 
forest f6(f);
forest f7(f);
iterator f6_aunt(adobe::find(adobe::preorder_range(f6), "aunt").base());
 
std::cout << "Size of f6 pre-splice: " << f6.size() << std::endl;
std::cout << "Size of f7 pre-splice: " << f7.size() << std::endl;
 
f6_aunt = adobe::trailing_of(f6_aunt);
 
// Note that because f6_aunt is on the trailing edge, the spliced forest's
// top nodes will be children to f6_aunt.
 
f6.splice(f6_aunt, f7);    
 
output(adobe::depth_range(f6));
 
std::cout << "Size of f6 post-splice: " << f6.size() << std::endl;
std::cout << "Size of f7 post-splice: " << f7.size() << std::endl;

Results:

Size of f6 pre-splice: 8
Size of f7 pre-splice: 8
<grandmother>
    <mother>
        <me>
        </me>
        <sister>
        </sister>
        <brother>
        </brother>
    </mother>
    <aunt>
        <cousin>
        </cousin>
        <grandmother>
            <mother>
                <me>
                </me>
                <sister>
                </sister>
                <brother>
                </brother>
            </mother>
            <aunt>
                <cousin>
                </cousin>
            </aunt>
            <uncle>
            </uncle>
        </grandmother>
    </aunt>
    <uncle>
    </uncle>
</grandmother>
Size of f6 post-splice: 16
Size of f7 post-splice: 0